Je ne sais plus exactement à quelle occasion j’ai entendu parler de Mickaël Launay, mathématicien et vulgarisateur; il me semble que c’est en regardant une émission à la TV, mais je ne me rappelle plus laquelle. J’ai donc acheté l’un de ses livres, intitulé « Le théorème du parapluie ». Ce livre est écrit sans formule mathématique (pour les amateurs, il y en a dans les annexes, mais il n’est pas nécessaire de les lire pour comprendre).
Les sujets abordés sont surprenants et même parfois contre-intuitifs. J’ai choisi aujourd’hui de vous parler du chapitre 1 intitulé.
« La loi des supermarchés ».
L’auteur nous emmène en voyage en direction du supermarché le plus proche. Mickaël Launay nous demande de lire toutes les étiquettes de produit rencontrées dans le supermarché.
Pendant cette lecture, on note uniquement le 1er chiffre du prix de chaque article. Par exemple:
- un article à 2,45 CHF, on note 2
- un article à 5,80 CHF, on note 5
- un article à 47,65 CHF, on note 4
- un article àn 0,75 CHF et on note cette fois le premier chiffre significatif: 7
Mickaël Launay a obtenu les résultats suivants après avoir noté le 1er chiffre de 1126 articles dans un supermarché en janvier 2019, selon la méthode indiquée plus haut:
- Il a noté 391 articles dont le prix commence par un « 1 » -> 31,9%
- 315 articles dont le prix commence par un « 2 » -> 25,7%
- 182 articles dont le prix commence par un « 3 » -> 14,8%
- 182 articles dont le prix commence par un « 4 » -> 8,8%
- 66 articles dont le prix commence par un « 5 » -> 5,4%
- 50 articles dont le prix commence par un « 6 » -> 4,1%
- 40 articles dont le prix commence par un « 7 » -> 3,3%
- 30 articles dont le prix commence par un « 8 » -> 2,4%
- 44 articles dont le prix commence par un « 9 »-> 3,6%
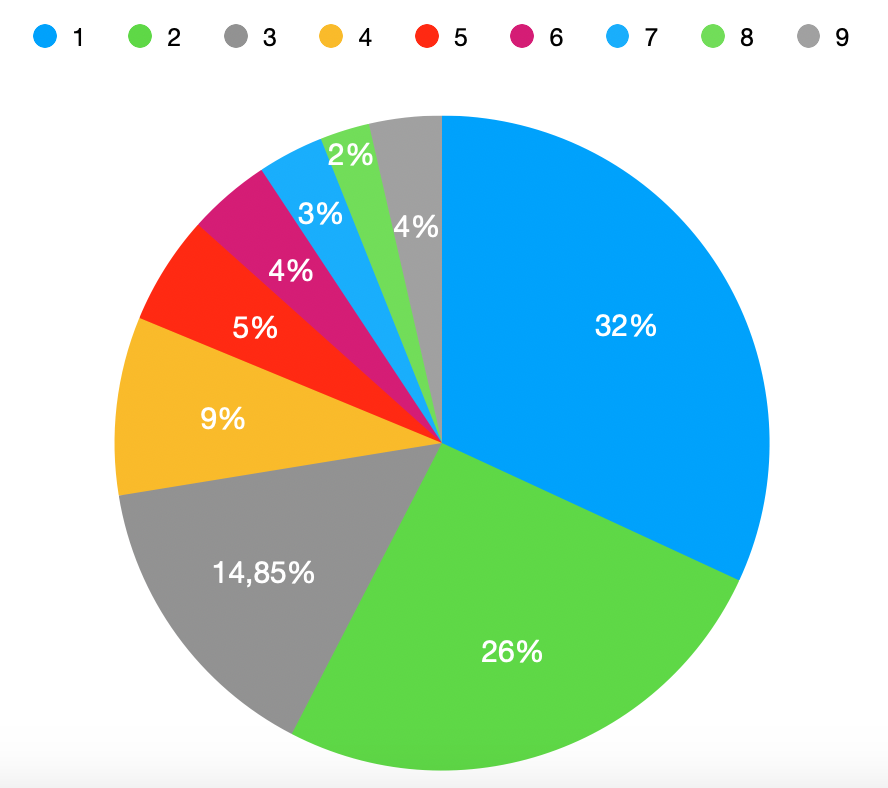
Le résultat peut paraître surprenant; pourquoi les premiers chiffres ne sont-ils apparemment pas équitablement répartis? Pourquoi y a-t-il beaucoup plus de prix commençant par un « 1 » que de prix commençant par un « 9 ». Si vous en avez le temps et l’envie, vous pouvez profiter d’une journée pluvieuse pour refaire la même expérience et vérifier que vous arrivez à peu près au même résultat.
En fait, l’ingénieur et physicien Frank Benford a analysé des données numériques issues de plus de 20’000 observations d’origines variées comprenant des longueurs de fleuves, les populations de plusieurs villes américaines, par exemple. Les répartitions des premiers chiffres des nombres étudiés suit une répartition proche de celle du supermarché de M. Launay. Il a publié un article en 1938 intitulé « The Law of Anomalous numbers ». Cette loi est maintenant connue sous le nom de « Loi de Benford » ou Loi de Newcomb-Benford ».
Alors, quelle est l’explication de cette répartition apparemment bizarre des premiers chiffres de données statistiques dans plein de domaines différents? La réponse se trouve dans le premier chapitre du livre « Le théorème du parapluie » de Mickaël Launay que je vous encourage à acheter ou à emprunter.
Je donne tout de même un indice: l’explication passe par l’usage des logarithmes. J’espère ne pas vous faire fuir à la vue du mot logarithme. Mes nombreuses années d’enseignement m’ont appris qu’il fallait toujours prendre des précautions pour introduire cette notion parce qu’une mauvaise compréhension de celle-ci laisse des traces dans toute la suite des études en mathématiques.
On retrouve le mot logarithme dans un chapelet d’injures du capitaine Haddock; c’est dire si le mot a mauvaise réputation!

Pour arriver à une compréhension meilleure de la loi de Benford l’auteur nous propose de questionner notre « sens inné des nombres », dans le paragraphe éponyme. Je vous invite à suivre l’auteur en prenant une feuille de papier, de tracer une droite horizontale, d’y marquer deux points (à une distance de 10 cm ou plus). Le point à gauche est étique mille (1’000) et le point le plus à droite sera étiqueté un milliard (1’000’000). Maintenant, l’auteur vous demande de placer le point que l’on marquera avec l’étiquette un million (1’000’000). Quel que soit le placement de votre point million, l’auteur vous demande de bien réfléchir à votre placement et à le justifier. Essayez, le résultat en vaut la peine!

Le texte ci-dessus est constitué d’extraits du 1er chapitre du livre « Le théorème du parapluie » de Mickaël Launay et de remarques personnelles qui je l’espère vous inciterons à entreprendre un petit voyage en pays mathématique. Suite au prochain épisode.
PS: en 1881, Simon Newcomb s’est aperçu de l’usure (et donc de l’utilisation) plus marquées des premières pages des tables de logarithmes et a rapporté ce fait dans article de l’American Journal of Mathematics. Cet article est passé inaperçu jusqu’en 1938.
